lunes, 31 de enero de 2011
domingo, 30 de enero de 2011
PRODUCTOS NOTABLES.
Se llama productos notables a ciertas expresiones algebraicas que se encuentran frecuentemente y que es preciso saber factorizarlas a simple vista; es decir, sin necesidad de hacerlo paso por paso.
A continuación veremos algunas expresiones y del lado derecho de la igualdad, la forma de factorizarlas.
Cuadrado de la suma de dos cantidades o binomio cuadrado
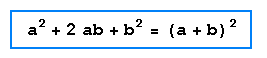 El cuadrado de la suma de dos cantidades es igual al cuadrado de la primera cantidad más el doble de la primera cantidad por la segunda más el cuadrado de la segunda cantidad.
El cuadrado de la suma de dos cantidades es igual al cuadrado de la primera cantidad más el doble de la primera cantidad por la segunda más el cuadrado de la segunda cantidad.
Demostración:
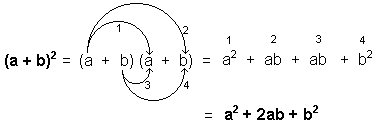
Ver: PSU; Matemática
Pregunta 12_2005
Cuadrado de la diferencia de dos cantidades
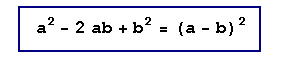 El cuadrado de la diferencia de dos cantidades es igual al cuadrado de la primera cantidad menos el doble de la primera cantidad por la segunda más el cuadrado de la segunda cantidad.
El cuadrado de la diferencia de dos cantidades es igual al cuadrado de la primera cantidad menos el doble de la primera cantidad por la segunda más el cuadrado de la segunda cantidad.
Demostración:
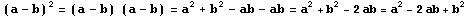 Producto de la suma por la diferencia de dos cantidades
Producto de la suma por la diferencia de dos cantidades
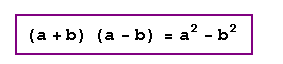 El producto de la suma por la diferencia de dos cantidades es igual al cuadrado de la primera cantidad menos el cuadrado de la segunda
El producto de la suma por la diferencia de dos cantidades es igual al cuadrado de la primera cantidad menos el cuadrado de la segunda
Demostración:
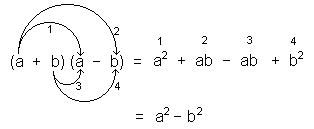 Ver: PSU: Matematica,
Ver: PSU: Matematica,
Pregunta 15_2010
Pregunta 19_2010
Otros casos:
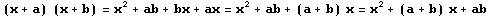
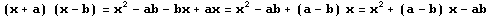
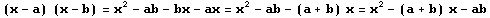
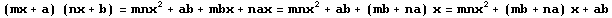 A modo de resumen, se entrega el siguiente cuadro con Productos notables:
A modo de resumen, se entrega el siguiente cuadro con Productos notables:
Fuentes Internet:
http://valle.fciencias.unam.mx/~rocio/factorizacion/factorizacion.html
http://www.memo.com.co/fenonino/aprenda/matemat/matematicas4.html
A continuación veremos algunas expresiones y del lado derecho de la igualdad, la forma de factorizarlas.
Cuadrado de la suma de dos cantidades o binomio cuadrado
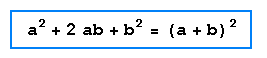
Demostración:
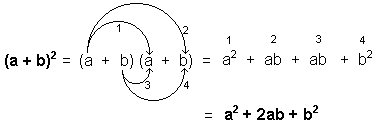
Pregunta 12_2005
Cuadrado de la diferencia de dos cantidades
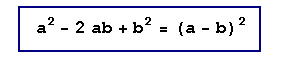
Demostración:
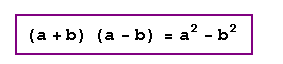
Demostración:
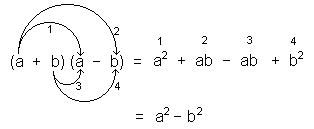
Pregunta 15_2010
Pregunta 19_2010
Otros casos:
1) 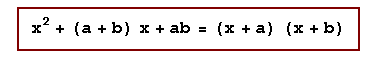
Demostración: 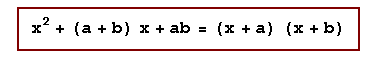
2) 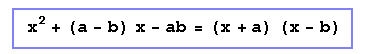
Demostración: 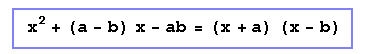
3) 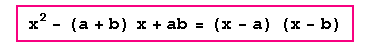
Demostración: 4)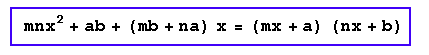
Demostración: 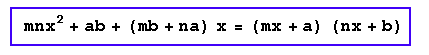
| (a + b)2 | = | a2 + 2ab + b2 | Binomio al cuadrado |
| (a + b)3 | = | a3 + 3a2b + 3ab2 + b3 | Binomio al cubo |
| a2 - b2 | = | (a + b) (a - b) | Diferencia de cuadrados |
| a3 - b3 | = | (a - b) (a2 + b2 + ab) | Diferencia de cubos |
| a3 + b3 | = | (a + b) (a2 + b2 - ab) | Suma de cubos |
| a4 - b4 | = | (a + b) (a - b) (a2 + b2) | Diferencia cuarta |
| (a + b + c)2 | = | a2 + b2 + c2 + 2ab + 2ac + 2bc | Trinomio al cuadrado |
Fuentes Internet:
http://valle.fciencias.unam.mx/~rocio/factorizacion/factorizacion.html
http://www.memo.com.co/fenonino/aprenda/matemat/matematicas4.html
ECUACIONES.
Una ecuación es una igualdad que sólo se verifica para unos valores concretos de una variable, generalmente llamada x.
Resolver una ecuación consiste en hallar los valores de la variable que hacen cierta la igualdad.
Recuerda:
Si un elemento está sumando en un miembro pasa al otro restando. Si está restando pasa sumado.
Si un número multiplica a todos los elementos de un miembro pasa al otro dividiendo y si los divise pasa multipllicando.
Resolver una ecuación consiste en hallar los valores de la variable que hacen cierta la igualdad.
Recuerda:
Si un elemento está sumando en un miembro pasa al otro restando. Si está restando pasa sumado.
Si un número multiplica a todos los elementos de un miembro pasa al otro dividiendo y si los divise pasa multipllicando.
ALGEBRA.
El álgebra es la rama de las matematicas que estudia las estructuras, las relaciones y las cantidades (en el caso del álgebra elemental). Es una de las principales ramas de la matemática, junto a la geometria, el analisis matematica, la combinatoria y la teoria de numeros.
La palabra «álgebra» es de origen árabe, deriva del tratado escrito por el matemático persaMuhammad ibn Musa al-Jwarizmi , titulado Kitab al-yabr wa-l-muqabala (que significa "Compendio de cálculo por el método de completado y balanceado"), el cual proporcionaba operaciones simbólicas para la solución sistemática de ecuaciones lineales y cuadraticas. etimologicamente, la palabra «álgebra»ر(yabr) , proviene del arabe y significa "reducción".
La palabra «álgebra» es de origen árabe, deriva del tratado escrito por el matemático persaMuhammad ibn Musa al-Jwarizmi , titulado Kitab al-yabr wa-l-muqabala (que significa "Compendio de cálculo por el método de completado y balanceado"), el cual proporcionaba operaciones simbólicas para la solución sistemática de ecuaciones lineales y cuadraticas. etimologicamente, la palabra «álgebra»ر(yabr) , proviene del arabe y significa "reducción".
Suscribirse a:
Entradas (Atom)
